Mozaika Penrose'a, czyli jak architekci z Azji Środkowej przewidzieli odkrycie europejskich naukowców o pięć wieków. Mozaika Penrose'a i starożytne islamskie wzory symetryczna mozaika
Mozaika Penrose'a, płytki Penrose'a - nieokresowe układanie płaszczyzny, aperiodyczne regularne struktury, układanie płaszczyzny z rombami dwóch rodzajów - o kątach 72 ° i 108 ° („grube romby”) oraz 36 ° i 144 ° („cienkie romby”), takie (proporcje są zgodne ze „złotym podziałem”), że dowolne dwa sąsiednie (czyli mające wspólną stronę) romb nie tworzą razem równoległoboku.Nazwany na cześć Rogera Penrose'a, który interesował się problemem „kafelkowania”, czyli wypełniania płaszczyzny figurami o tym samym kształcie bez przerw i zakładek.
Wszystkie takie kafelki są nieokresowe i lokalnie izomorficzne względem siebie (to znaczy każdy skończony fragment jednej kafelki Penrose'a występuje w każdym innym). „Samopodobieństwo” – można łączyć sąsiadujące ze sobą płytki mozaiki w taki sposób, aby ponownie stworzyć mozaikę Penrose.
Na każdej z dwóch płytek można narysować kilka segmentów, tak aby po ułożeniu mozaiki końce tych segmentów nachodziły na siebie i na płaszczyźnie utworzyło się kilka rodzin równoległych linii prostych (pasków Ammana).
Odległości między sąsiednimi liniami równoległymi przyjmują dokładnie dwie różne wartości (a dla każdej rodziny linii równoległych sekwencja tych wartości jest samopodobna).
Mozaiki Penrose'a, które mają otwory, pokrywają całą płaszczyznę, z wyjątkiem figury o skończonej powierzchni. Nie da się powiększyć otworu poprzez usunięcie kilku (skończonych) płytek, po czym nie da się całkowicie wybrukować odsłoniętej części.
Problem rozwiązuje układanie płytek z figurami, które tworzą okresowo powtarzający się wzór, ale Penrose chciał znaleźć właśnie taką figurę, która układając samolot, nie tworzyłaby powtarzających się wzorów. Uważano, że nie ma takich kafli, z których zbudowane zostałyby jedynie nieokresowe mozaiki. Penrose ręcznie wybrał wiele płytek o różnych kształtach, w rezultacie były tylko 2 z nich, posiadające „złotą proporcję”, która jest podstawą wszystkich harmonijnych relacji. Są to kształty romboidalne o kątach 108 ° i 72 °. Później figury zostały uproszczone do postaci prostego rombu (36° i 144°), opartego na zasadzie „złotego trójkąta”.
Powstałe wzory mają formę quasikrystaliczną, która ma symetria osiowa Piąte zamówienie. Struktura mozaikowa jest powiązana z ciągiem Fibonacciego.
(
Wikipedia)


Mozaika Penrose'a. Biały punkt oznacza środek symetrii obrotowej piątego rzędu: obrót o 72° wokół niego przenosi mozaikę w siebie.
Łańcuchy i mozaiki (Dziennik Nauka i Życie, 2005 nr 10)
Najpierw rozważ następujący wyidealizowany model. Niech cząstki w równowadze będą usytuowane wzdłuż osi transportu z i utworzą liniowy łańcuch z zmienny okres, zmieniające się zgodnie z prawem postępu geometrycznego:
аn = a1 Dn-1,
gdzie a1 - okres początkowy między cząstkami, n to liczba porządkowa okresu, n = 1, 2,…, D = (1 + √5) / 2 = 1,6180339… to liczba złotego podziału.
Skonstruowany łańcuch cząstek służy jako przykład jednowymiarowego quasikryształu o dalekosiężnym porządku symetrii. Struktura jest absolutnie uporządkowana, istnieje systematyczny układ cząstek na osi – ich współrzędne określa jedno prawo. Jednocześnie nie ma nawrotów - okresy między cząstkami są różne i cały czas się wydłużają. Uzyskana struktura jednowymiarowa nie ma zatem symetrii translacyjnej, a przyczyną tego nie jest chaotyczny układ cząstek (jak w strukturach amorficznych), ale irracjonalny stosunek dwóch sąsiednich okresów (D to liczba niewymierna).
Logiczną kontynuacją rozważanej jednowymiarowej struktury quasikryształu jest struktura dwuwymiarowa, którą można opisać metodą konstruowania nieokresowych mozaik (wzorów) składających się z dwóch różnych elementów, dwóch komórek elementarnych. Ta mozaika została opracowana w 1974 roku przez fizyka teoretycznego z Uniwersytetu Oksfordzkiego R. Penrose'a. Znalazł mozaikę dwóch rombów o równych bokach. Wewnętrzne kąty wąskiego rombu wynoszą 36 ° i 144 °, a szerokiego romb to 72 ° i 108 °.
Kąty tych rombów są związane ze złotym podziałem, który wyraża się algebraicznie równaniem x2 - x - 1 = 0 lub równaniem y2 + y - 1 = 0. Pierwiastki tych równań kwadratowych można zapisać w postaci trygonometrycznej :
x1 = 2cos36°, x2 = 2cos108°,
y1 = 2cos72 °, y2 = cos144 °.
Ta niekonwencjonalna forma przedstawienia pierwiastków równań pokazuje, że te romby można nazwać wąskimi i szerokimi złotymi rombami.
W mozaice Penrose'a płaszczyzna pokryta jest złotymi rombami bez przerw i zakładek, i może być nieskończenie rozłożona na długość i szerokość. Aby jednak zbudować nieskończoną mozaikę, należy przestrzegać pewnych zasad, które znacznie różnią się od monotonnego powtarzania się tych samych komórek elementarnych, z których składa się kryształ. Jeśli naruszona zostanie zasada dopasowania złotych rombów, to po pewnym czasie wzrost mozaiki ustanie, ponieważ pojawią się nieodwracalne niespójności.
W niekończącej się mozaice Penrose'a złote romby układają się bez ścisłej okresowości. Jednak stosunek liczby szerokich złotych rombów do liczby wąskich złotych rombów jest dokładnie równy złotej liczbie D = (1 + √5) / 2 = = 1,6180339…. Ponieważ liczba D jest niewymierna, w takiej mozaice nie można wyodrębnić komórki elementarnej o całkowitej liczbie rombów każdego typu, których translacja mogłaby uzyskać całą mozaikę.
Mozaika Penrose'a ma swój szczególny urok jako przedmiot zabawnej matematyki. Nie wchodząc we wszystkie aspekty tego zagadnienia, zauważamy, że już pierwszy krok – budowanie mozaiki – jest dość interesujący, ponieważ wymaga uwagi, cierpliwości i pewnej pomysłowości. I wiele inwencji i wyobraźni można pokazać, jeśli zrobisz mozaikę wielokolorową. Kolorystykę, która natychmiast zamienia się w grę, można wykonać licznymi oryginalne sposoby, których warianty przedstawiono na rysunkach (poniżej). Biała kropka oznacza środek mozaiki, obrót o 72° wokół niej wprowadza ją w siebie.
Mozaika Penrose'a jest doskonałym przykładem na to, jak piękna konstrukcja, znajdująca się na skrzyżowaniu różnych dyscyplin, z pewnością zostanie wykorzystana. Jeśli punkty węzłowe zostaną zastąpione atomami, mozaika Penrose'a stanie się dobrym analogiem dwuwymiarowego quasikryształu, ponieważ ma wiele właściwości charakterystycznych dla takiego stanu materii. I własnie dlatego.
Po pierwsze, budowa mozaiki realizowana jest według pewnego algorytmu, w wyniku którego okazuje się, że jest to nie losowa, a uporządkowana struktura. Każda jego skończona część pojawia się w całej mozaice niezliczoną ilość razy.
Po drugie, w mozaice można wyróżnić wiele regularnych dziesięciokątów o dokładnie takich samych orientacjach. Tworzą dalekosiężny porządek orientacyjny zwany quasiperiodycznym. Oznacza to, że istnieje interakcja między odległymi strukturami mozaikowymi, która godzi lokalizację i względną orientację diamentów w dobrze określony, choć niejednoznaczny sposób.
Po trzecie, jeśli konsekwentnie zamalujesz wszystkie romby bokami równoległymi do dowolnego wybranego kierunku, tworzą one ciąg łamanych linii. Wzdłuż tych przerywanych linii można narysować proste równoległe linie, oddalone od siebie w przybliżeniu w tej samej odległości. Dzięki tej właściwości możemy mówić o pewnej symetrii translacyjnej w kafelkach Penrose'a.
Po czwarte, kolejno wypełnione rombami tworzą pięć rodzin podobnych równoległych linii, przecinających się pod kątami będącymi wielokrotnościami 72 °. Kierunki tych linii przerywanych odpowiadają kierunkom boków pięciokąta foremnego. Dlatego mozaika Penrose'a ma do pewnego stopnia symetrię obrotową piątego rzędu iw tym sensie jest podobna do quasikryształu.
Wstyd! Ludzie średniowiecza przewyższali współczesnych naukowców. Myśleliśmy, że naszym osiągnięciem jest zaawansowana matematyka i krystalografia. Okazuje się, że nic w tym rodzaju - wszystko to było już pół tysiąca lat temu. Ponadto wydaje się, że współczesną naukę wyprzedzili nie najlepsi matematycy, ale prości artyści. No, może nie bardzo proste... Ale jednak!
Nie, cóż, w rzeczywistości - współcześni matematycy zajmują się czystym nonsensem! Następnie papier jest składany 12 razy, następnie równania Lorenza są szydełkowane, a następnie kulki są skręcane w pączki. Ogólnie rzecz biorąc, z poważnych ludzi pozostał tylko Perelman i Okunkow - cała nadzieja jest w nich ...
Interesujące jest jednak to, że w starożytności ludzie dokonywali matematycznych osiągnięć, czasem nie przywiązując do nich szczególnej wagi. Interesujące jest również to, że naukowcy powtarzają dziś te same „stare” odkrycia, nie podejrzewając wcale, że wymyślają coś, co istniało bez ich domysłów od ponad wieku.
Na przykład angielski matematyk Roger Penrose wymyślił coś takiego w 1973 roku - specjalną mozaikę o geometrycznych kształtach. W związku z tym stała się mozaiką Penrose'a. Co jest w tym tak konkretnego?
Mozaika Penrose'a w wersji jej twórcy. Składa się z dwóch rodzajów rombów, jednego o kącie 72 stopni, drugiego o kącie 36 stopni. Obraz z niego okazuje się symetryczny, ale nie okresowy (ilustracja ze strony en.wikipedia.org).
Mozaika Penrose to wzór składający się z wielokątnych płytek o dwóch określonych kształtach (nieco różne romby). Mogą wybrukować nieskończoną płaszczyznę bez przerw.
Powstały obraz wygląda, jakby był rodzajem „rytmicznego” ornamentu - obrazka o symetrii translacyjnej. Ten rodzaj symetrii oznacza, że we wzorze można wybrać pewien kawałek, który można „skopiować” na płaszczyźnie, a następnie połączyć te „duplikaty” ze sobą poprzez przeniesienie równoległe (czyli bez rotacji i bez powiększenia).
Jeśli jednak przyjrzeć się bliżej, można zauważyć, że we wzorze Penrose'a nie ma takich powtarzalnych struktur – jest to aperiodyczne. Ale nie chodzi o złudzenie optyczne, ale o to, że mozaika nie jest chaotyczna: ma symetrię obrotową piątego rzędu.

Przykładami quasi-stali są stop AlMnPd i Al 60 Li 30 Cu 10 (ilustracja Paul J. Steinhardt).
Oznacza to, że obraz można obracać pod minimalnym kątem 360 / n stopnie gdzie n- kolejność symetrii, w tym przypadku n= 5. Zatem kąt obrotu, który niczego nie zmienia, musi być wielokrotnością 360/5 = 72 stopnie.
Przez około dekadę wynalazek Penrose'a był uważany za niewiele więcej niż uroczą abstrakcję matematyczną. Jednak w 1984 roku Dan Shechtman, profesor izraelskiego Instytutu Technologicznego (Technion), badając strukturę stopu aluminiowo-magnezowego, odkrył, że na siatce atomowej tej substancji zachodzi dyfrakcja.
Wcześniejsze koncepcje fizyki ciała stałego wykluczały taką możliwość: struktura obrazu dyfrakcyjnego ma symetrię piątego rzędu. Jego części nie można łączyć transferem równoległym, co oznacza, że w ogóle nie jest kryształem. Ale dyfrakcja jest charakterystyczna tylko dla sieci krystalicznej!
Jak tu być? Pytanie nie jest łatwe, więc naukowcy zgodzili się, że ta opcja będzie nazywana quasikryształami - czymś w rodzaju specjalnego stanu skupienia.

Pokazano tutaj jeden z wzorów płytek przedstawionych w XV-wiecznym arabskim rękopisie. Naukowcy podkreślili powtarzające się obszary kolorami. Wszystkie wzory geometryczne średniowiecznych mistrzów arabskich studiowane przez Lou i Steinhardta opierają się na tych pięciu elementach. Jak widać, powtarzające się elementy niekoniecznie pokrywają się z granicami płytek (ilustracja Peter J. Lu).
Cóż, całe piękno tego odkrycia, zgadliście, polega na tym, że model matematyczny był na to od dawna gotowy. I, jak zapewne zrozumiałeś, jest to mozaika Penrose'a. Ale ten nie ma wcale dziesięciu lat, ale znacznie więcej. Stało się to znane dopiero w naszych czasach, na początku XXI wieku, a ten model okazał się znacznie starszy niż można sobie wyobrazić.
W 2007 roku Peter J. Lu, fizyk z Harvard University, połączył siły z innym fizykiem, Paulem J. Steinhardtem, ale z Princeton University, aby opublikować artykuł w Science o mozaikach. Penrose (Lou powinien być znany stałym czytelnikom „Membranes " - rozmawialiśmy już o jego odkryciach diamentowego cięcia starożytnych siekier i najbardziej skomplikowanych starych maszyn). Wydawałoby się, że nie ma tu wiele nieoczekiwanego: odkrycie quasikryształów wzbudziło żywe zainteresowanie tym tematem, co doprowadziło do pojawienia się w prasie naukowej masy publikacji.
Najważniejszym punktem pracy jest jednak to, że nie jest ona poświęcona nowoczesna nauka... I ogólnie - nie nauka.

Wzory „kwazikrystaliczne” znalazły swoje miejsce nie tylko w architekturze. Tutaj można zobaczyć okładkę Koranu z lat 1306-1315 oraz rysunek fragmentów geometrycznych, na których opiera się wzór. Ten i następne przykłady nie odpowiadają sieciom Penrose'a, ale mają obrotową symetrię piątego rzędu (ilustracja Petera J. Lu).
Lu zwrócił uwagę na wzory pokrywające meczety w Azji, budowane w średniowieczu. Te łatwo rozpoznawalne projekty są wykonane z mozaiki. Nazywane są girihi (od arabskiego słowa oznaczającego „węzeł”) i są geometrycznym wzorem charakterystycznym dla sztuki islamu i składają się z wielokątów.
Przez długi czas wierzono, że te wzory powstają za pomocą linijki i cyrkla. Jednak kilka lat temu, podróżując po Uzbekistanie, Lu zainteresował się mozaikowymi wzorami, które zdobiły lokalną średniowieczną architekturę i zauważył w nich coś znajomego.
Wracając na Harvard, naukowiec zaczął rozważać podobne motywy w mozaikach na ścianach średniowiecznych budowli w Afganistanie, Iranie, Iraku i Turcji.
Odkrył, że te wzory są prawie takie same i był w stanie podkreślić podstawowe elementy żyrihów używanych we wszystkich projektach geometrycznych. Ponadto znalazł rysunki tych obrazów w starożytnych rękopisach, które starożytni artyści wykorzystywali jako rodzaj ściągawki do ozdabiania ścian.
Ale okazuje się, że to wszystko nie jest tak ważne. Do tworzenia tych wzorów używali nie prostych, losowo wymyślonych konturów, ale figury ułożone w określonej kolejności. I nie jest to szczególnie zaskakujące.
Co ciekawe, zapomniawszy o takich schematach, ludzie spotkali się z nimi ponownie później. Tak, tak, starożytne wzory to nic innego jak to, co wieki później zostanie nazwane sieciami Penrose'a i zostanie znalezione w strukturze quasikryształów!

Te same obszary są uwydatnione na tych obrazach, chociaż są to fotografie z różnych meczetów (ilustracja Peter J. Lu).
W tradycji islamskiej obowiązywał surowy zakaz wizerunku ludzi i zwierząt, dlatego wzory geometryczne stały się bardzo popularne w projektowaniu budynków. Średniowiecznym rzemieślnikom udało się jakoś to zmienić. Ale jaki był sekret ich „strategii” – nikt nie wiedział. Sekretem okazuje się więc użycie specjalnych mozaik, które, pozostając symetryczne, mogą wypełniać płaszczyznę bez powtarzania.
Inną "sztuczką" tych obrazów jest to, że artyści "kopiując" takie schematy w różnych kościołach według rysunków, nieuchronnie musieliby przyznać się do przekłamań. Ale tego rodzaju naruszenia są minimalne. Wyjaśnia to tylko fakt, że rysunki na dużą skalę nie miały sensu: najważniejsza jest zasada budowania obrazu.
Do montażu żyrichów użyto płytek pięciu rodzajów (rombów dziesięcio- i pięciokątnych oraz „motyli”), które wykonano w mozaikę przylegającą do siebie bez wolnej przestrzeni między nimi. Stworzone z nich mozaiki mogły mieć jednocześnie zarówno symetrię obrotową, jak i translacyjną, a jedynie symetrię obrotową piątego rzędu (czyli były to mozaiki Penrose'a).

Fragment ornamentu irańskiego mauzoleum z 1304 roku. Po prawej stronie znajduje się rekonstrukcja żyrichów (ilustracja Peter J. Lu).
Po zbadaniu setek fotografii średniowiecznych zabytków muzułmańskich Lou i Steinhardt byli w stanie datować podobny trend do XIII wieku. Stopniowo metoda ta stawała się coraz bardziej popularna i do XV wieku stała się powszechna.
Badacze uznali sanktuarium Imama Darb-i w irańskim mieście Isfahan z 1453 roku za przykład niemal idealnej struktury quasi-krystalicznej.
To odkrycie zrobiło wrażenie na wielu osobach. Amerykańskie Stowarzyszenie na rzecz Postępu Nauki (
Uczestnicy projektu
Nikiforov Kirill, uczeń klasy 8
Rudneva Oksana, uczennica klasy 8
Poturaeva Ksenia, uczennica klasy 8
Temat badań
Mozaika Penrose'a
Problematyczne pytanie
Czym jest mozaika Penrose'a?
Hipoteza badawcza
Istnieje nieokresowe kafelkowanie samolotu
Cele badań
Poznaj mozaikę Penrose'a i dowiedz się, dlaczego nazywa się ją „złotą” mozaiką
Wyniki
Mozaika Penrose'a
Dachówka płaszczyzny to pokrycie całej płaszczyzny nienakładającymi się na siebie kształtami. W matematyce problem pełnego wypełnienia płaszczyzny wielokątami bez przerw i zakładek nazywamy parkietami lub mozaikami. Prawdopodobnie pierwsze zainteresowanie brukowaniem pojawiło się w związku z budową mozaik, ozdób i innych wzorów. Nawet starożytni Grecy wiedzieli, że problem ten można łatwo rozwiązać, pokrywając płaszczyznę regularnymi trójkątami, kwadratami i sześciokątami.
Takie kafelkowanie samolotu nazywa się okresowym. Później nauczyli się, jak wykonać kafelkowanie za pomocą kombinacji kilku regularnych wielokątów.

Trudniejszym zadaniem było wykonanie nie do końca „poprawnego” lub „prawie” okresowego parkietu. Przez długi czas uważano, że ten problem nie ma rozwiązania. Jednak w latach 60. ubiegłego wieku nadal był rozwiązany, ale wymagało to zestawu tysięcy wielokątów różne rodzaje... Stopniowo zmniejszano liczbę gatunków, aż wreszcie w połowie lat 70. profesor Uniwersytetu Oksfordzkiego Roger Penrose, wybitny naukowiec naszych czasów, aktywnie działający w różnych dziedzinach matematyki i fizyki, rozwiązał problem przy użyciu tylko dwóch rodzajów rombów.
Roger Penrose
Zbadaliśmy metodę konstruowania takiej mozaiki, którą obecnie nazywamy mozaiką Penrose'a. Aby to zrobić, narysuj przekątne w pięciokąt foremny (pięciokąt). Otrzymujemy - nowy pięciokąt i dwa rodzaje trójkątów równoramiennych, które nazywane są „złotymi”. Stosunek uda do podstawy w takich trójkątach jest równy „złotemu” stosunkowi. Kąty w trójkątach wynoszą 36 °, 72 ° i 72 ° w jednym oraz 108 °, 36 ° i 36 ° w drugim. Połączmy dwa identyczne trójkąty i zdobądźmy „złote” romb. Naukowiec wykorzystał je przy projektowaniu parkietu, a sam parkiet nazwano „złotym”.
Mozaika Penrose'a
Mozaika Penrose posiada właściwości:
1. stosunek liczby cienkich rombów do liczby grubych jest zawsze równy tak zwanej „złotej” liczbie 1,618 ...
I starożytniislamskie wzorce
Prezentacja została wykonana przez
uczeń klasy 7B Centralnego Ośrodka Szkolno-Wychowawczego nr 1679
Gerder Marina.
Liderzy projektów
Sinyukova E.V. i Zherder V.M.
5klass.net
Czym jest mozaika
Mozaika prezentywzorzec,
zmontowane z płytek
różne kształty. Przez nich
może być utwardzony
nieskończony
samolot bez
spacje. Mozaika okresowa to mozaika,
którego rysunek jest powtarzany przez
równe odstępy.
Mozaika nieokresowa to mozaika,
który wzór można powtórzyć
w nieregularnych odstępach czasu.
Mozaiki w przyrodzie
Istnieje również wiele przykładów w przyrodzie.okresowa mozaika. Głównie
kryształy ciał stałych - np.:
Kryształ soli
Diamentowy kryształ
Kryształ grafitowy
Kryształ grafenu
Mozaiki na obrazach Eschera
Mozaiki są ważnym tematem wSztuka. Artysta
M.K. Escher jest znany ze swojego
mozaiki i nie prawdziwe
obrazy.
Czym jest mozaika Penrose'a?
W 1973język angielski
matematyk Roger
Penrose (Roger
Penrose) utworzono
specjalna mozaika
z geometrycznych
liczby, które i
stał się znany jako mozaika Penrose'a.
Wielokątne płyty mozaikowe
Mozaika Penrose'a jestmozaika złożona z wielokąta
płytki o dwóch określonych kształtach.
Symetria mozaiki
Wynikowy obraz wygląda jakjakby to był jakiś „rytmiczny”
ozdoba - obrazek,
posiadanie
translacyjne
symetria.
Symetria
Symetria translacyjna oznaczaco we wzorze możesz wybrać?
pewien kawałek, który możesz
„skopiuj” w samolocie, a potem
połącz te „duplikaty” ze sobą
transfer równoległy.
10. Struktura mozaiki
Jeśli jednak przyjrzysz się uważnie, możeszzobacz, że takich nie ma
powtarzające się struktury - to
nieokresowe. Ale w ogóle nie chodzi o
złudzenie optyczne, ale to mozaika
nie chaotyczna: ona
posiada
rotacyjny
symetria piątego
zamówienie.
11. Minimalny kąt
To znaczy, żeobraz może
włączyć
minimalny kąt,
równy 360/n stopni,
gdzie n jest porządkiem
symetria, w tym
przypadek n = 5.
Dlatego kąt
obracając to nic
nie zmienia się, powinien być
wielokrotność 360/5 = 72
stopnie.
12. Niezwykłe zjawisko
W 1984 DanShechtman robi
studium konstrukcji
stop aluminiowo-magnezowy,
znalazłem to na
sieć atomowa
tej substancji
dziać się
niezwykłe dla
kryształy
zjawisko fizyczne.
13. „Niewłaściwe” kryształy
Próbka substancji poddanejspecjalna metoda szybkiego
chłodzenie, rozpraszanie wiązki elektronów
tak, że uformowała się płyta fotograficzna
wyraźny
dyfrakcyjny
obraz z symetrią
piąty rząd w
Lokalizacja
dyfrakcyjny
wzloty
(symetria dwudziestościanu).
14. Quasikryształy
Naukowcy zgodzili sięto podane
opcją byłoby
Nazwa
kwazikryształy -
coś specjalnego
stan rzeczy. ORAZ
dla niego przez długi czas
był gotowy
model matematyczny
- Mozaika Penrose'a.
15.
Publikacja 2007W 2007 roku fizycy Peter Lou i Paul
Steinhardt opublikowany w czasopiśmie
Artykuł naukowy o mozaikach
Penrose'a.
16. Zainteresowanie quasikryształami
Pozornie,nieoczekiwane tutaj
trochę: otwarcie
quasikryształy
przyciągnął żywy
zainteresowanie tym
temat, który prowadził
do wyglądu stosu
publikacje w
prasa naukowa.
17. Wzory w Azji
Najważniejszym punktem pracy jest jednak to, żenie jest poświęcony współczesnej nauce.
I ogólnie - nie nauka. Piotr Lou
zwrócił uwagę na wzory,
obejmujące meczety
w Azji, zbudowany
w średniowieczu.
18.
Style. GiriW islamskim ozdobie są dwa
styl:
Girikh (os.) - trudny
ornament geometryczny,
skomponowany ze stylizowanych in
prostokątne i wielokątne
kształty linii. W większości przypadków
używany do zewnętrznych
dekoracja meczetów i księgi w dużej ilości
wydanie.
19. Islimi
Islimi (os.) - rodzaj ozdoby,zbudowany na styku powój i
spirale. Wcielenia w stylizowanych
czyli naturalistyczna forma pomysłu
stale rozwijające się kwitnienie
pęd liściasty. Najwspanialszy
rozprzestrzenił się w ubraniach,
książki, dekoracja wnętrz meczetów,
naczynia.
20. Mozaiki Uzbekistanu
Podczas podróży wUzbekistan, Lu zainteresował się wzorami
mozaiki, które zdobiły lokalne
średniowieczna architektura i zauważona w
im coś znajomego.
Okładka Koranu 13061315 i
rysunek
geometryczny
paprochy,
na którym
wzorzec.
21. Mozaiki z różnych krajów
Z powrotem wHarvard, naukowiec został
rozważać
podobne motywy w
mozaiki na ścianach
średniowieczny
Budynki
Afganistan, Iran,
Irak i Turcja.
22. Mozaiki islamskie
Ta próbka jest datowana na późniejszą datę.okres - 1622 (meczet indyjski).
23. Schematy girihs
Peter Lou odkrył tę geometrięschematy girih są praktycznie takie same i
potrafił podkreślić główne elementy,
używane we wszystkich
ozdoby geometryczne. Ponadto,
rysunki tych obrazów znalazł w
starożytne rękopisy, które…
starożytni artyści lubili
jako rodzaj ściągawki dla
dekoracja ścienna.
24. Zbuduj zamówienie
Aby stworzyć te wzory, nieproste, losowo wymyślone kontury,
oraz figury, które znajdowały się w
pewien porządek. Starożytne wzory
okazały się dokładnymi konstrukcjami mozaiki
Penrose!
25.
tradycje islamskieW tradycji islamskiej
był surowy
zakaz obrazu
ludzie i zwierzęta,
dlatego w projekcie
budynki duże
zyskał popularność
geometryczny
ornament.
26. Sekret starożytnych mistrzów
Średniowieczni rzemieślnicyzrobiłem to?
urozmaicony. Ale co
był ich sekretem
"strategie" - nikt
wiedział. Tak więc sekret polega na tym, jak
kiedy się okaże
za pomocą
specjalne mozaiki,
kto może zostać?
symetryczny,
wypełnić samolot, nie
powtórzenie.
27. „skupienie”
Kolejna „sztuczka” z nich„Skupienie” obrazów polega na tym,
„kopiując” takie schematy do
różne świątynie w
rysunki, artyści
nieuchronnie musiałby
pozwalają na zniekształcenia. Ale
naruszenie tego
charakter są minimalne.
Wyjaśnia to tylko fakt
że mistrzowie nie są
używane rysunki, gdy
budowanie mozaiki.
28. Płytki
Do montażu girihsużywane płytki od pięciu
gatunki (dziesięć i
romb pięciokątny i
"motyle"), które w
skompilowano mozaiki,
przylegające do siebie
bez wolnego
spacje między
ich.
29. Symetria mozaik
Mozaiki z nich wykonane,może zostać opętany tak szybko, jak to możliwe
rotacyjny i
translacyjne
symetria i tylko
symetria obrotowa
piąty rząd (tj.
były mozaiki?
Penrose'a).
30. Girihi
Fragment ornamentu irańskiego mauzoleum1304 lata. Po prawej - rekonstrukcja żyrikhów
31. Data pojawienia się mozaiki
Badam setkiData
pozory
zdjęcia
mozaiki
średniowieczny
muzułmański
wdzięki kobiece,
Lou i Steinhardt byli w stanie
data pojawienia się
podobny trend XIII
stulecie. Stopniowo to
sposób, w jaki zdobyłem wszystko
duża popularność i do
XV wiek stał się powszechny
pospolity.
32. Płytki ceramiczne
Randki w przybliżeniupokrywa się z okresem
rozwój technologii
ozdabianie
pałace, meczety,
różne ważne
budynki przeszklone
kolor
płytek ceramicznych
w postaci różnych
wielokąty. To
mieć ceramikę
specjalne płytki
utworzone formularze
specjalnie dla żyrików.
Ceramiczny
płytka
33. Wniosek
Co odkryła zachodnia naukana podstawie ogromnego uogólnienia
cierniste doświadczenie, nauka orientalna
wykonane w oparciu o intuicję i uczucie
Piękny. A wyniki są oczywiste: in
ucieleśnienie praw geometrii w
praktykować myślicieli orientalnych
wyprzedzając Zachód o pięć wieków!
W 1973 roku angielski matematyk Roger Penrose stworzył specjalną mozaikę o geometrycznych kształtach, która stała się znana jako mozaika Penrose'a.
Mozaika Penrose to wzór składający się z wielokątnych płytek o dwóch określonych kształtach (nieco różne romby). Mogą wybrukować nieskończoną płaszczyznę bez przerw.
Mozaika Penrose'a w wersji jej twórcy.
Składa się z dwóch rodzajów rombów,
jeden na 72 stopnie, drugi na 36 stopni.
Obraz jest symetryczny, ale nie okresowy.
Powstały obraz wygląda, jakby był rodzajem „rytmicznego” ornamentu - obrazka o symetrii translacyjnej. Ten rodzaj symetrii oznacza, że można wybrać we wzorze określony element, który można „skopiować” na płaszczyźnie, a następnie te „duplikaty” można połączyć ze sobą poprzez przeniesienie równoległe (czyli bez rotacji i bez rozszerzenie).
Jeśli jednak przyjrzeć się bliżej, można zauważyć, że we wzorze Penrose'a nie ma takich powtarzalnych struktur – jest to aperiodyczne. Ale nie chodzi o złudzenie optyczne, ale o to, że mozaika nie jest chaotyczna: ma symetrię obrotową piątego rzędu.
Oznacza to, że obraz można obrócić o minimalny kąt 360/n stopni, gdzie n jest rzędem symetrii, w tym przypadku n = 5. Zatem kąt obrotu, który niczego nie zmienia, musi być wielokrotnością 360/5 = 72 stopnie.
Przez około dekadę wynalazek Penrose'a był uważany za niewiele więcej niż uroczą abstrakcję matematyczną. Jednak w 1984 roku Dan Shechtman, profesor izraelskiego Instytutu Technologicznego (Technion), badając strukturę stopu aluminiowo-magnezowego, odkrył, że na siatce atomowej tej substancji zachodzi dyfrakcja.
Wcześniejsze koncepcje fizyki ciała stałego wykluczały taką możliwość: struktura obrazu dyfrakcyjnego ma symetrię piątego rzędu. Jego części nie można łączyć transferem równoległym, co oznacza, że w ogóle nie jest kryształem. Ale dyfrakcja jest charakterystyczna tylko dla sieci krystalicznej! Naukowcy zgodzili się, że ta opcja będzie nazywana quasikryształami - czymś w rodzaju specjalnego stanu materii. Cóż, całe piękno odkrycia polega na tym, że model matematyczny był już na to gotowy - mozaika Penrose'a.
I całkiem niedawno stało się jasne, że ta matematyczna konstrukcja ma znacznie więcej lat, niż można sobie wyobrazić. W 2007 roku Peter J. Lu, fizyk z Harvard University, połączył siły z innym fizykiem, Paulem J. Steinhardtem, ale z Princeton University, aby opublikować artykuł w Science o mozaikach Penrose. Wydawałoby się, że nie ma tu wiele nieoczekiwanego: odkrycie quasikryształów wzbudziło żywe zainteresowanie tym tematem, co doprowadziło do pojawienia się w prasie naukowej masy publikacji.
Najważniejszym punktem pracy jest jednak to, że nie jest ona poświęcona współczesnej nauce. I ogólnie - nie nauka. Peter Lu zwrócił uwagę na wzory pokrywające meczety w Azji, budowane w średniowieczu. Te łatwo rozpoznawalne projekty są wykonane z mozaiki. Nazywane są girihi (od arabskiego słowa oznaczającego „węzeł”) i są geometrycznym wzorem charakterystycznym dla sztuki islamu i składają się z wielokątów.

Wzór kafelkowy przedstawiony w XV-wiecznym rękopisie arabskim.
Naukowcy podkreślili powtarzające się obszary kolorami.
Wszystkie wzory geometryczne budowane są w oparciu o te pięć elementów.
średniowieczni mistrzowie arabscy. Powtarzające się elementy
niekoniecznie pasują do granic płytek.
W ornamentach islamskich wyróżnia się dwa style: geometryczny – girih i kwiatowy – islimi.
Giri(os.) - złożony ornament geometryczny złożony z linii stylizowanych na figury prostokątne i wielokątne. W większości przypadków służy do projekt zewnętrzny meczety i książki w dużym nakładzie.
Islimi(os.) - rodzaj ornamentu zbudowanego na połączeniu powoju i spirali. Uosabia w stylizowanej lub naturalistycznej formie ideę stale rosnącego, kwitnącego pędu liściastego i obejmuje nieskończoną różnorodność opcji. Jest najczęściej stosowany w odzieży, książkach, dekoracji wnętrz meczetów i naczyniach.

Okładka Koranu 1306-1315 i rysunek fragmentów geometrycznych,
na którym opiera się wzór. Ten i poniższe przykłady nie pasują do siebie
Kraty Penrose'a, ale mają obrotową symetrię piątego rzędu
Przed odkryciem Petera Lou wierzono, że starożytni architekci tworzyli wzory girih za pomocą linijki i cyrkla (jeśli nie intuicyjnie). Jednak kilka lat temu, podróżując po Uzbekistanie, Lu zainteresował się mozaikowymi wzorami, które zdobiły lokalną średniowieczną architekturę i zauważył w nich coś znajomego. Wracając na Harvard, naukowiec zaczął rozważać podobne motywy w mozaikach na ścianach średniowiecznych budowli w Afganistanie, Iranie, Iraku i Turcji.

Ta próbka jest datowana na późniejszy okres - 1622 (indyjski meczet).
Patrząc na niego i rysując jego strukturę, nie można nie podziwiać ciężkiej pracy
badacze. I oczywiście sami mistrzowie.
Peter Lou odkrył, że geometryczne wzory girichów są praktycznie takie same i był w stanie podkreślić podstawowe elementy używane we wszystkich geometrycznych wzorach. Ponadto znalazł rysunki tych obrazów w starożytnych rękopisach, które starożytni artyści wykorzystywali jako rodzaj ściągawki do ozdabiania ścian.
Do tworzenia tych wzorów używali nie prostych, losowo wymyślonych konturów, ale figury ułożone w określonej kolejności. Starożytne wzory okazały się wiernymi konstrukcjami mozaiki Penrose'a!

Na tych zdjęciach podświetlone są te same obszary,
chociaż są to zdjęcia z różnych meczetów
W tradycji islamskiej obowiązywał surowy zakaz wizerunku ludzi i zwierząt, dlatego wzory geometryczne stały się bardzo popularne w projektowaniu budynków. Średniowiecznym rzemieślnikom udało się jakoś to zmienić. Ale jaki był sekret ich „strategii” – nikt nie wiedział. Sekretem okazuje się więc użycie specjalnych mozaik, które, pozostając symetryczne, mogą wypełniać płaszczyznę bez powtarzania.
Inną "sztuczką" tych obrazów jest to, że artyści "kopiując" takie schematy w różnych kościołach według rysunków, nieuchronnie musieliby przyznać się do przekłamań. Ale tego rodzaju naruszenia są minimalne. Wyjaśnia to tylko fakt, że rysunki na dużą skalę nie miały sensu: najważniejsza jest zasada budowania obrazu.
Do montażu żyrichów użyto płytek pięciu rodzajów (rombów dziesięcio- i pięciokątnych oraz „motyli”), które ułożono w mozaikę przylegającą do siebie bez wolnej przestrzeni między nimi. Stworzone z nich mozaiki mogły mieć jednocześnie zarówno symetrię obrotową, jak i translacyjną, a jedynie symetrię obrotową piątego rzędu (czyli były to mozaiki Penrose'a).

Fragment ornamentu irańskiego mauzoleum z 1304 roku. Po prawej - rekonstrukcja żyrikhów
Po zbadaniu setek fotografii średniowiecznych zabytków muzułmańskich Lou i Steinhardt byli w stanie datować podobny trend do XIII wieku. Stopniowo metoda ta stawała się coraz bardziej popularna i do XV wieku stała się powszechna. Datowanie z grubsza pokrywa się z okresem rozwoju techniki zdobienia pałaców, meczetów, różnych ważnych budowli glazurowanymi kolorowymi płytkami ceramicznymi w postaci różnych wielokątów. Oznacza to, że specjalnie dla żyrichów stworzono płytki ceramiczne o specjalnych kształtach.
Badacze uznali sanktuarium Imama Darb-i w irańskim mieście Isfahan z 1453 roku za przykład niemal idealnej struktury quasi-krystalicznej.

Portal sanktuarium imama Darb-i w Isfahanie (Iran).
Tutaj dwa systemy girihów nakładają się na siebie jednocześnie.

Kolumna dziedzińca meczetu w Turcji (ok. 1200)
oraz mury medres w Iranie (1219). To są wczesne prace
i używają tylko dwóch elementów konstrukcyjnych znalezionych przez Lu
Teraz pozostaje znaleźć odpowiedzi na wiele tajemnic z historii mozaiki girih i Penrose. Jak i dlaczego starożytni matematycy odkryli struktury quasikrystaliczne? Czy średniowieczni Arabowie nadawali mozaikom jakiekolwiek znaczenie poza artystycznym? Dlaczego tak interesująca koncepcja matematyczna została zapomniana na pół tysiąclecia? A co najciekawsze - jakie inne współczesne odkrycia są nowe, które w rzeczywistości jest dobrze zapomnianym starym?
Popularny
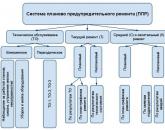
- Konserwacja prewencyjna i jej rola w produkcji
- Planowana konserwacja prewencyjna sprzętu
- O procedurze umieszczania niestacjonarnych obiektów handlu sezonowego
- Przepisy dotyczące umieszczania niestacjonarnych obiektów handlowych
- Malowanie dekoracyjne w przedszkolu „magiczne loki” to wspólne działanie nauczyciela i
- Opis organizacji i prowadzenia zajęć z rozwoju poznawczego w drugiej grupie juniorów „Pokarm dla ptaków
- Nowe zawody Gdzie uzyskać informacje o odpowiednich specjalistach
- Diplodok z plasteliny. Lekcja rzeźbienia. Jak łatwo wykonać podstawowe kształty z plasteliny: kulka, stożek, walec, warkocz, cegła Jak zrobić walec z plasteliny
- Ocena agencji rekrutacyjnych
- Ocena agencji rekrutacyjnych